WebGL2 - Un cubo y una pirámide
Created at: 2023-04-01
Tercer tutorial de la serie de artículos dedicados a WebGL en su segunda versión. Ha llegado el momento de dibujar nuestras primeras figuras en 3D, y conocer un poco mejor cómo funciona el fragment shader cuando necesita calcular el color de cada píxel.

Este es el resultado donde podemos ver dos figuras 3D rotando en el espacio.
Aquí tienes el enlace al repositorio con todo el código de esta serie de tutoriales.
Como siempre, juega un rato con él antes de continuar leyendo este tutorial. Así te será más fácil entender cómo funciona el chiringuito.
Interpolaciones lineales
Pero antes de entrar en materia, vamos a explicar un poco mejor como funciona el envío de variables de tipo varying entre el vertex shader y el fragment shader. Me encanta hacer spoilers en los subtítulos del tutorial, y ahora acabo de hacerte otro. La pregunta que puede que te hayas hecho en algún momento es... ¿Cómo diantres sabe el fragment shader la posición del puñetero píxel que va a dibujar, si en su código GLSL no le llega nada del vertex shader? Bueno, aparentemente no le llega nada... pero por debajo el motor de WebGL ha calculado la coordenada exacta del píxel a dibujar ejecutando una interpolación lineal entre todos los vértices implicados en el tipo de dibujado que has solicitado. Y aunque no es necesario usarla, el fragment shader puede obtener el valor de la coordenada concreta que va a colorear a través de la variable de tipo vec4 gl_FragCoord y usarla de algún modo para calcular el color, si le interesa.
¿Qué es una interpolación lineal? Pues es una especie de valor ponderado en un punto concreto, conocidos previamente un grupo de valores límite. Ese punto concreto es un valor normalizado entre 0 y 1. Por ejemplo, para una dimensión y dados unos valores límite de 5 y de 10, el resultado de una interpolación para el punto 0 el resultado es 5. Para el punto 1, el resultado es 10. Para el punto 0.1, el resultado es 5.5, y para el punto 0.5, el resultado es 7.5. Esta operación también se puede hacer para vectores de dos, tres y cuatro dimensiones. WebGL sabe calcularlas para todos los casos.
Como dije en el primer tutorial, webgl, técnicamente, solo sabe dibujar puntos, líneas y triángulos, con algunas pequeñas variaciones. Si usas el tipo punto, el programa web gl consumirá un bloque del búfer de datos de las coordenadas, y a continuación llamará una vez al vertex shader una sola vez con esa coordenada, para calcular la coordenada "real". A continuación, llamará una sola vez al fragment shader.
Si se quiere dibujar una línea, entonces el programa consumirá dos bloques, llamará dos veces al vertex shader, para calcular dos coordenadas "reales", y ejecutará una serie de interpolaciones lineales, en un proceso conocido como rasterización para conocer un listado de coordenadas suavizadas finales que definen la línea. Cada una de esas coordenadas obtenidas, que pueden llegar a ser muchísimas, supone una ejecución del fragment shader sobre ella para determinar el color de su pixel.
Y en caso de que el modo de dibujado sea el de triángulo o sus variantes, donde se consumirán dos o tres bloques según el modo de dibujado, se llamará al vertex shader tres veces, una por vértice del triángulo, y durante el proceso de rasterización, más complicado que el anterior, se harán muchas interpolaciones lineales que acabarán calculando todas las coordenadas encerradas en el área definida por el triángulo, y como siempre, se ejecutará el fragment shader para cada una de ellas para calcular su color.
Pues bien, como comentamos en el primer tutorial, el vertex shader también puede mandarle variables al fragment shader, llamadas varying. ¿Qué valor tendrá cada una de ellas en una ejecución concreta del fragment shader? Pues acabará haciendo algo muy parecido a lo que hace con las coordenadas, pero esta vez ejecutando la interpolación lineal entre todos los valores límite de la variable varying enviada.
Para ver un ejemplo práctico, voy a crear un escenario sencillo: dibujaré un triángulo gigante que no se mueve en el centro de la pantalla. Como no aporta nada en este ejemplo, eliminaré todo rastro de matrices y transformaciones. La novedad consiste en enviar esta vez el color a través del atributo a_color mediante otro búfer de datos, donde enviaré el color de cada coordenada. Luego, el vertex shader la leerá y se la mandará al fragment shader sin modificar, mediante una variable varying v_color. Recuerda que la cantidad de bloques de cada uno de los búferes debe ser el mismo, si no quieres tener problemas. Eso sí, el tamaño de bloque puede ser diferente en cada búfer.
En ejemplos anteriores, el color lo enviábamos directamente al fragment shader usando para ello una variable uniforme. Como recordatorio, estas variables eran una especie de constante global para toda la ejecución del programa en un ciclo de renderizado.
Así pues, partiendo del código del primer tutorial, lo he modificado con los siguientes cambios que ya deberías de entender y seguir sin demasiados problemas:
'use strict'
class Engine {
#ctx;
constructor(canvas) {
const vertexShaderSource = `#version 300 es
precision highp float;
in vec3 a_position;
in vec4 a_color;
out vec4 v_color;
void main() {
gl_Position = vec4(a_position, 1);
v_color = a_color;
}
`;
const fragmentShaderSource = `#version 300 es
precision highp float;
in vec4 v_color;
out vec4 color;
void main() {
color = v_color;
}
`;
// ...
}
// ...
#drawAll(program) {
this.#ctx.viewport(0, 0, this.#ctx.canvas.width, this.#ctx.canvas.height);
const positionAttr = this.#ctx.getAttribLocation(program, 'a_position');
const colorAttr = this.#ctx.getAttribLocation(program, 'a_color');
this.#clear();
this.#ctx.enableVertexAttribArray(positionAttr);
this.#ctx.enableVertexAttribArray(colorAttr);
this.#drawTriangle(positionAttr, colorAttr);
this.#ctx.disableVertexAttribArray(positionAttr);
this.#ctx.disableVertexAttribArray(colorAttr);
}
#drawTriangle(positionAttr, colorAttr) {
const coordsBlockSize = 2;
const coords = new Float32Array([
-0.8, 0.8,
0.8, -0.8,
-0.8, -0.8
]);
const colorsBlockSize = 4;
const colors = new Float32Array([
1, 0, 0, 1,
0, 1, 0, 1,
0, 0, 1, 1
]);
const totalBlocks = coords.length / coordsBlockSize;
this.#ctx.bindBuffer(this.#ctx.ARRAY_BUFFER, this.#ctx.createBuffer());
this.#ctx.bufferData(this.#ctx.ARRAY_BUFFER, coords, this.#ctx.STATIC_DRAW);
this.#ctx.vertexAttribPointer(positionAttr, coordsBlockSize, this.#ctx.FLOAT, false, 0, 0);
this.#ctx.bindBuffer(this.#ctx.ARRAY_BUFFER, this.#ctx.createBuffer());
this.#ctx.bufferData(this.#ctx.ARRAY_BUFFER, colors, this.#ctx.STATIC_DRAW);
this.#ctx.vertexAttribPointer(colorAttr, colorsBlockSize, this.#ctx.FLOAT, false, 0, 0);
this.#ctx.drawArrays(this.#ctx.TRIANGLES, 0, totalBlocks);
}
}
Es interesante notar que en el vertex shader, la varying variable la tipamos como out, pero el fragment shader usamos in.
Y este es el resultado:

Estás viendo visualmente (válgase la redundancia) el resultado de la interpolación lineal entre los colores primarios rojo, azul y verde, definidos en el búfer de datos colors, uno por vértice. El resultado de la interpolación lineal de cada punto sobre los colores límite, es el color que se está dibujando ese píxel. Puedes notar que los puntos más cercanos al vértice, su color es más intenso y cercano al del color del vértice, uno de los valores límite, y que conforme se aleja, se va mezclando poco a poco con el del valor o valores límite más cercanos. En este enlace tienes el ejemplo funcionando.
¿Cómo puedo dibujar el triángulo de un solo color como hacíamos en ejemplos anteriores? Fácil, asigna el mismo color a cada vértice. Repito una vez más, a causa de cómo son leídos por el vertex shader del programa webgl2, todos los búferes de datos tienen que tener el mismo número de bloques, así que has de enviarlo tres veces, porque es el número de bloques que hemos dicho que vamos a enviar, cuando llamamos a drawArrays. No puedes evitar que se hagan tropecientas interpolaciones innecesarias, pero no te preocupes, la GPU está optimizada para ello y no pondrá pegas. Aquí puedes ver el resultado.
Álgebra segunda parte.
Una vez que te hayas cansado de estrujarte los sesos hasta pensar que ya lo entiendes, podemos darle otra vuelta de tuerca al tema y complicarlo un pelín más antes de acabar el día.
Si para dibujar polígonos en 2D necesitábamos una clase que sepa operar matrices 3X3, nadie se sorprenderá si comento que para hacer lo mismo en 3D necesitamos otra para matrices 4X4. Aunque con una novedad respecto a las rotaciones.
Para refrescar conceptos, en 2D teníamos un eje de coordenadas x e y, que corresponden con la posición del vértice que queremos dibujar en el eje horizontal, y con su posición en el eje vertical. En 3D tenemos un eje de 3 dimensiones x, y y z, para indicar su posición horizontal, vertical y profundidad. Igual que pasaba con los ejes x e y, el eje z también está restringido a un rango dibujable de -1 a +1, decreciendo hacia adelante (es decir, desde la pantalla hacía tí), y creciendo hacia atrás. Como con los otros ejes, nos interesa usar píxeles en nuestro código JS, y que nuestro método de nuestra clase matriz se siga encargando de traducirlo.
Si lo meditas, en 2D estábamos rotando las figuras sobre su eje z. Si no eres capaz de verlo, imagina que rotar consiste en atravesar su coordenada (0, 0) con un palillo y hacerla girar como una peonza. ¿Lo ves ahora?. Y sí, lo hacíamos sobre el eje z, a pesar de estar en un contexto supuestamente 2D. La realidad es que estábamos dibujando polígonos planos en un contexto 3D, donde todas las coordenadas z estaban harcodeadas a 1 en el vertex shader. Girar en el eje x o y no tendría mucho sentido en 2D, pues el polígono se voltearía hacia adelante, en el caso del eje x, o hacia los lados, en el caso del eje y, y visualmente se vería cómo se encoge hasta quedar como una línea de un solo píxel antes de volver a estirarse. Piensa de nuevo en el ejemplo del palillo pero atravesando la figura de arriba a abajo, o de derecha a izquierda, para imaginar lo que ocurre.
Sin embargo, este tipo de rotación en 3D es una opción deseable. Por lo tanto, vamos a crear transformaciones de rotación sobre cada eje. Para la de z basta con renombrar la que ya tenemos hecha. Para las otras es suficiente con seguir multiplicando por matrices de transformación que contiene unos, senos y cosenos ordenados de forma diferente.
Trasladar o escalar no tiene mucho misterio. Hay que añadirles un tercer argumento que indique el valor de la operación en la coordenada z y a correr.
Y en cuanto a la resolución, la cosa se complica mucho si realmente queremos resolver de forma definitiva el problema. Para renderizar mundos 3D, conceptos que en 2D eran irrelevantes, ahora son fundamentales. Hablar de resolución en 3D como hacíamos en ejemplos anteriores no es suficiente. Si queremos gestionar el tema completamente, tendríamos que tener en cuenta conceptos como la perspectiva, y todo lo que implica.
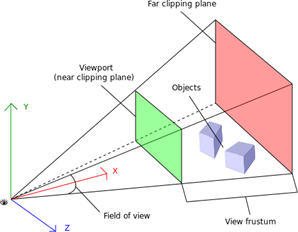
Para definir la perspectiva ya no solo importa el escenario, es decir, la posición de las figuras del mundo que queremos dibujar. Ahora es igual de importante tener en cuenta el concepto de cámara y sus múltiples características. Las más importantes son:
- La coordenada donde está.
- El campo de visión FOV que tiene.
- El espacio a renderizar (view frustum).
- El tipo de proyección usada.
De momento mantendremos las cosas sencillas, así que seguiremos sin concretar el concepto de cámaras y perspectivas. Seguiremos siendo continuístas con el enfoque del método resolution anterior, que correspondería a una cámara en la coordenada (0, 0) mirando de frente el escenario con un campo de visión que mantiene el mismo ratio que el canvas sobre el que estamos renderizando, y usando una proyección ortogonal, lo cual significa que no hay distorsión de la figura en profundidad. Esto quiere decir que no importa la profundidad a la que se encuentra la figura, es decir, el valor de su coordenada z, siempre se dibujará con el mismo tamaño. Me limitaré a escalar también z de forma similar a lo hecho en las otros ejes, por el valor que me pasen en depth.
Tal vez profundice en la definición de la cámara en futuros tutoriales, si yo mismo soy capaz de comprenderlo del todo...
Pero volvamos al turrón, he aquí la nueva clase Matrix4 con la implementación final. Como dije, los cambios son continuístas con lo que teníamos, pero aplicando lo explicado anteriormente.
'use strict'
class Matrix4 {
#matrix;
constructor(matrix) {
this.#matrix = matrix;
}
get matrix() {
return this.#matrix;
}
rotateX(rad) {
const c = Math.cos(rad);
const s = Math.sin(rad);
this.#matrix = this.#multiply(
[
1, 0, 0, 0,
0, c, -s, 0,
0, s, c, 0,
0, 0, 0, 1
]
);
return this;
}
rotateY(rad) {
const c = Math.cos(rad);
const s = Math.sin(rad);
this.#matrix = this.#multiply(
[
c, 0, s, 0,
0, 1, 0, 0,
-s, 0, c, 0,
0, 0, 0, 1
]
);
return this;
}
rotateZ(rad) {
const c = Math.cos(rad);
const s = Math.sin(rad);
this.#matrix = this.#multiply(
[
c, -s, 0, 0,
s, c, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1
]
);
return this;
}
scale(sx, sy, sz) {
this.#matrix = this.#multiply(
[
sx, 0, 0, 0,
0, sy, 0, 0,
0, 0, sz, 0,
0, 0, 0, 1
]
);
return this;
}
translate(tx, ty, tz) {
this.#matrix = this.#multiply(
[
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
tx, ty, tz, 1
]
);
return this;
}
resolution(width, height, depth) {
return this
.scale(2 / width, -2 / height, 2 / depth)
.translate(-1, 1, 0);
}
#multiply(other) {
return [
this.#matrix[0] * other[0] + this.#matrix[1] * other[4] + this.#matrix[2] * other[8] + this.#matrix[3] * other[12],
this.#matrix[0] * other[1] + this.#matrix[1] * other[5] + this.#matrix[2] * other[9] + this.#matrix[3] * other[13],
this.#matrix[0] * other[2] + this.#matrix[1] * other[6] + this.#matrix[2] * other[10] + this.#matrix[3] * other[14],
this.#matrix[0] * other[3] + this.#matrix[1] * other[7] + this.#matrix[2] * other[11] + this.#matrix[3] * other[15],
this.#matrix[4] * other[0] + this.#matrix[5] * other[4] + this.#matrix[6] * other[8] + this.#matrix[7] * other[12],
this.#matrix[4] * other[1] + this.#matrix[5] * other[5] + this.#matrix[6] * other[9] + this.#matrix[7] * other[13],
this.#matrix[4] * other[2] + this.#matrix[5] * other[6] + this.#matrix[6] * other[10] + this.#matrix[7] * other[14],
this.#matrix[4] * other[3] + this.#matrix[5] * other[7] + this.#matrix[6] * other[11] + this.#matrix[7] * other[15],
this.#matrix[8] * other[0] + this.#matrix[9] * other[4] + this.#matrix[10] * other[8] + this.#matrix[11] * other[12],
this.#matrix[8] * other[1] + this.#matrix[9] * other[5] + this.#matrix[10] * other[9] + this.#matrix[11] * other[13],
this.#matrix[8] * other[2] + this.#matrix[9] * other[6] + this.#matrix[10] * other[10] + this.#matrix[11] * other[14],
this.#matrix[8] * other[3] + this.#matrix[9] * other[7] + this.#matrix[10] * other[11] + this.#matrix[11] * other[15],
this.#matrix[12] * other[0] + this.#matrix[13] * other[4] + this.#matrix[14] * other[8] + this.#matrix[15] * other[12],
this.#matrix[12] * other[1] + this.#matrix[13] * other[5] + this.#matrix[14] * other[9] + this.#matrix[15] * other[13],
this.#matrix[12] * other[2] + this.#matrix[13] * other[6] + this.#matrix[14] * other[10] + this.#matrix[15] * other[14],
this.#matrix[12] * other[3] + this.#matrix[13] * other[7] + this.#matrix[14] * other[11] + this.#matrix[15] * other[15]
];
}
static identity() {
return new Matrix4(
[
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1
]
);
}
}
Cambios en el programa
En los tutoriales anteriores, el tema del color de la figura lo solucionábamos por la vía directa, mediante una variable uniforme u_color. Para este nuevo ejemplo podríamos hacer lo mismo, pero como no tenemos ni luces ni sombras, todas las caras se verían exactamente con el mismo color, y la animación sería confusa al no poder distinguirse claramente dónde empieza y acaba cada cara. Me ha parecido más interesante e incluso imprescindible dibujar las caras con colores diferentes, sirviéndome como excusa para utilizar nuevas herramientas que nos brinda el API.
Este es nuestro nuevo programa:
'use strict'
class Engine {
// ...
constructor(canvas) {
const vertexShaderSource = `#version 300 es
precision highp float;
in vec3 a_position;
in vec4 a_color;
uniform mat4 u_transform;
out vec4 v_color;
void main() {
gl_Position = u_transform * vec4(a_position, 1);
v_color = a_color;
}
`;
const fragmentShaderSource = `#version 300 es
precision highp float;
in vec4 v_color;
out vec4 color;
void main() {
color = v_color;
}
`;
// ...
}
#drawAll() {
this.#ctx.enable(this.#ctx.DEPTH_TEST);
this.#ctx.viewport(0, 0, this.#ctx.canvas.width, this.#ctx.canvas.height);
const positionAttr = this.#ctx.getAttribLocation(this.#program, 'a_position');
const colorAttr = this.#ctx.getAttribLocation(this.#program, 'a_color');
const transformUniform = this.#ctx.getUniformLocation(this.#program, 'u_transform');
this.#ctx.enableVertexAttribArray(positionAttr);
this.#ctx.enableVertexAttribArray(colorAttr);
this.#drawLoop(positionAttr, colorAttr, transformUniform,);
}
#drawLoop(positionAttr, colorAttr, transformUniform) {
this.#clear();
this.#drawPyramid(positionAttr, colorAttr, transformUniform);
this.#drawCube(positionAttr, colorAttr, transformUniform);
window.requestAnimationFrame(() => this.#drawLoop(positionAttr, colorAttr, transformUniform));
}
#clear() {
this.#ctx.clearColor(0, 0, 0, 1);
this.#ctx.clear(this.#ctx.COLOR_BUFFER_BIT | this.#ctx.DEPTH_BUFFER_BIT);
}
// ...
}
La novedad más importante es que el color lo hemos convertido a una variable de tipo atributo a_color, pasándole este valor al fragment shader mediante la variable varying v_color, exactamente igual que hicímos en el ejemplo de las interpolaciones lineales con la que empezábamos el capítulo. El otro cambio interesante es que nuestro a_position es una coordenada 3D, así que la recibimos directamente como un tipo vec3 ahorrándonos harcodear su z. Por los mismos motivos, la matriz de transformación está tipada como mat4.
Otra novedad interesante: Hay que decirle a webgl que tenga en cuenta la profundidad para dibujar los elementos. Esto se traduce a que objetos con un Z más pequeño se dibujan por delante de elementos que tengan un Z más grande. Si tienes nociones de CSS, este comportamiento es similar a z-index. Para activarlo, tenemos que indicarlo explícitamente mediante el método enable con el valor DEPTH_TEST, y luego, al limpiar la pantalla, resetear también el búfer interno de webgl añadiendo el flag DEPTH_BUFFER_BIT en el método clear. Te recomiendo trastear el código y probar a quitar esta configuración, a ver qué pasa.
Por último, hemos renombrado los métodos de dibujado de cada figura a drawPyramid y drawCube, más ajustados a la nueva realidad.
Definiendo y coloreando un cubo
Dibujar una figura 3D implica definir muchísimos más vértices que con una figura 2D, como es obvio. Además, por nuestra intención de dibujar cada cara de un color diferente, también estamos obligados a usar otro búfer de datos que contenga el color de cada uno de los vértices, como vimos en el primer ejemplo de este artículo. Por lo tanto, y como no me canso de señalar, tendríamos dos búferes de datos con obligatoriamente la misma cantidad de bloques, uno para las coordenadas de los vértices, y otro para sus colores. Podríamos seguir usando el modo TRIANGLE_STRIP para dibujar triángulos, pero cuando se tienen dos o más búferes de datos, puede volverse imposible seguir por este camino. El motivo es que probablemente uno de los búferes necesite contener un valor diferente para una misma coordenada, cuando esta es dibujada también en otra cara. Lo más práctico es curarse en salud y usar TRIANGLES a secas, a costa de tener que repetir algunos vértices de una misma cara entre dos o tres veces.
Pero para que crear el polígono no sea entonces aún más tedioso, Webgl2 nos proporciona un tipo de búfer que mencinamos en el primer capítulo pero que no hemos usado hasta ahora: el búfer de índices, que webgl llama ELEMENT_ARRAY_BUFFER. Por defecto, Webgl lee los bloques en el mismo orden en el que están dentro de los búferes. Si definimos un búfer de este tipo y se lo pedimos a webgl, el motor lo recorrerá secuencialmente y usará el valor leído como el índice de la posición del bloque a leer contenido en todos los búferes de datos definidos. Por tanto, podemos deducir que este búfer solo puede contener números enteros, que la longitud de este búfer corresponde con el total de bloques a leer, y que cada posición definida en este búfer de índices debe ser la posición de un bloque válido en todos los búferes de datos. Este búfer no necesita ningún nuevo atributo en el vertex shader, el trabajo de extraer su valor y saber cómo recuperar los bloques de los otros búferes es trabajo interno de webgl.
Veámos un pequeño ejemplo de cómo usar el búfer de índices para que quede todo un poco mas claro.
Imagina que tengo un cuadrado definido por los vértices A, B, C y D, y quiero dibujarlas con el color Z usando el modo TRIANGLES. El búfer de datos con las coordenadas contendría [A, B, C, B, C, D], y el búfer de datos con los colores [Z, Z, Z, Z, Z, Z].
Si quiero dibujar lo mismo, pero usando un búfer de índices, este contendría [0, 1, 2, 1, 2, 3], el búfer de datos con las coordenadas sería [A, B, C, D] y el búfer de colores [Z, Z, Z, Z], ahorrándome un 33% de bloques repetidos.
Con toda esta nueva información, ya estás listo para comprender cómo funciona el siguiente código, donde definimos un cubo:
'use strict'
class Engine {
// ...
#drawCube(positionAttr, colorAttr, transformUniform) {
const coordBlockSize = 3;
const coords = new Float32Array([
// Front face
-0.5, -0.5, -0.5,
0.5, -0.5, -0.5,
0.5, 0.5, -0.5,
-0.5, 0.5, -0.5,
// Back face
0.5, -0.5, 0.5,
-0.5, -0.5, 0.5,
-0.5, 0.5, 0.5,
0.5, 0.5, 0.5,
// Top face
-0.5, -0.5, 0.5,
0.5, -0.5, 0.5,
0.5, -0.5, -0.5,
-0.5, -0.5, -0.5,
// Bottom face
-0.5, 0.5, -0.5,
0.5, 0.5, -0.5,
0.5, 0.5, 0.5,
-0.5, 0.5, 0.5,
// Left face
0.5, -0.5, -0.5,
0.5, -0.5, 0.5,
0.5, 0.5, 0.5,
0.5, 0.5, -0.5,
// Right face
-0.5, -0.5, 0.5,
-0.5, -0.5, -0.5,
-0.5, 0.5, -0.5,
-0.5, 0.5, 0.5
]);
const coordIndex = new Uint16Array([
0, 1, 2, 0, 2, 3, // Front face
4, 5, 6, 4, 6, 7, // Back face
8, 9, 10, 8, 10, 11, // Top face
12, 13, 14, 12, 14, 15, // Bottom face
16, 17, 18, 16, 18, 19, // Left face
20, 21, 22, 20, 22, 23 // Right face
]);
const colorBlockSize = 4;
const colors = new Float32Array(
[]
.concat(this.#repeatColor([0.23, 0.56, 0.78, 1], 4)) // Front face
.concat(this.#repeatColor([0.12, 0.87, 0.45, 1], 4)) // Back face
.concat(this.#repeatColor([0.85, 0.65, 0.12, 1], 4)) // Top face
.concat(this.#repeatColor([0.27, 0.76, 0.62, 1], 4)) // Bottom face
.concat(this.#repeatColor([0.91, 0.53, 0.14, 1], 4)) // Left face
.concat(this.#repeatColor([0.32, 0.67, 0.86, 1], 4)) // Right face
);
const transform = Matrix4.identity()
.scale(100, 100, 100)
.rotateX(Date.now() / -1000)
.rotateY(Date.now() / -1000)
.rotateZ(Date.now() / -1000)
.translate(90, 310, 0)
.resolution(this.#width, this.#height, 200);
this.#ctx.bindBuffer(this.#ctx.ARRAY_BUFFER, this.#ctx.createBuffer());
this.#ctx.bufferData(this.#ctx.ARRAY_BUFFER, coords, this.#ctx.STATIC_DRAW);
this.#ctx.vertexAttribPointer(positionAttr, coordBlockSize, this.#ctx.FLOAT, false, 0, 0);
this.#ctx.bindBuffer(this.#ctx.ARRAY_BUFFER, this.#ctx.createBuffer());
this.#ctx.bufferData(this.#ctx.ARRAY_BUFFER, colors, this.#ctx.STATIC_DRAW);
this.#ctx.vertexAttribPointer(colorAttr, colorBlockSize, this.#ctx.FLOAT, false, 0, 0);
this.#ctx.bindBuffer(this.#ctx.ELEMENT_ARRAY_BUFFER, this.#ctx.createBuffer());
this.#ctx.bufferData(this.#ctx.ELEMENT_ARRAY_BUFFER, coordIndex, this.#ctx.STATIC_DRAW);
this.#ctx.uniformMatrix4fv(transformUniform, false, transform.matrix);
this.#ctx.drawElements(this.#ctx.TRIANGLES, coordIndex.length, this.#ctx.UNSIGNED_SHORT, 0);
}
#repeatColor(color, times) {
return Array.from({length: times}).fill(color).flat();
}
}
El tamaño de bloque ahora es de 3, para enviar coordenadas 3d (x, y z), y las coordenadas del cubo no tienen mayor misterio que saber dónde colocarlas para formar un cubo en el espacio cuyo centro está en (0, 0, 0).
Los cambios clave son el uso del nuevo búfer de tipo ELEMENT_ARRAY_BUFFER que guardamos en coordIndex, y que usamos drawElements en lugar de drawArrays para renderizar la escena pidiéndole a webgl que lo use. Todos los otros cambios son más o menos los esperables. Por comodidad, también he creado una pequeña función privada repeatColor para hacer lo que su nombre indica.
El último punto destacable son los usos de Matrix4 para añadir la nueva dimensión a todos los métodos. Es interesante recordar lo que dije de la proyección ortogonal: Si pruebas a modificar translate con una coordenada z diferente, el cubo se verá con el mismo tamaño. Ya veremos en futuros tutoriales cómo arreglar este problema.
Tal vez, algún avispado lector se percate de que aun usando un búfer de índices, sigo repitiendo algunas coordenadas en los búferes de datos. ¿Por qué no usar la misma? La razón es la misma por la que usar TRIANGLES_STRIP: Recuerda que el fichero de índices afecta a todos los búferes de datos, no solo al que contiene las coordenadas. Estamos relacionando cada vértice con un color distinto, así que si usáramos el mismo índice, y ese vértice se usara en caras diferentes, se usaría el mismo color en esas dos caras del cubo, produciendo el efecto de arco iris del ejemplo anterior, efecto que ahora no me interesa.
Definiendo y coloreando una pirámide
La solución es similar. Calculamos coordenadas y colores de la pirámide con una base cuadrada, y generamos el búfer de índices acorde. Detente a observar cómo hemos jugado con índices y bloques para conseguir dibujar tres caras triangulares de 3 vértices, y una cara cuadrada de 4 vértices.
'use strict'
class Engine {
// ...
#drawPyramid(positionAttr, colorAttr, transformUniform) {
const coordBlockSize = 3;
const coords = new Float32Array([
// Front face
0.0, 0.5, 0.0,
-0.5, -0.5, -0.5,
0.5, -0.5, -0.5,
// Right face
0.0, 0.5, 0.0,
0.5, -0.5, 0.5,
0.5, -0.5, -0.5,
// Back face
0.0, 0.5, 0.0,
0.5, -0.5, 0.5,
-0.5, -0.5, 0.5,
// Left face
0.0, 0.5, 0.0,
-0.5, -0.5, -0.5,
-0.5, -0.5, 0.5,
// Base
-0.5, -0.5, 0.5,
0.5, -0.5, 0.5,
0.5, -0.5, -0.5,
-0.5, -0.5, -0.5
]);
const coordIndex = new Uint16Array([
0, 1, 2, // Front face
3, 4, 5, // Right face
6, 7, 8, // Back face
9, 10, 11, // Left face
12, 13, 14, 12, 14, 15 // Base
]);
const colorBlockSize = 4;
const colors = new Float32Array(
[]
.concat(this.#repeatColor([0.93, 0.13, 0.55, 1], 3)) // Right face
.concat(this.#repeatColor([0.76, 0.23, 0.47, 1], 3)) // Right face
.concat(this.#repeatColor([0.42, 0.12, 0.78, 1], 3)) // Back face
.concat(this.#repeatColor([0.51, 0.25, 0.67, 1], 3)) // Left face
.concat(this.#repeatColor([0.98, 0.75, 0.04, 1], 4)) // Base
);
const transform = Matrix4.identity()
.scale(100, 100, 100)
.rotateX(Date.now() / 1000)
.rotateY(Date.now() / 1000)
.rotateZ(Date.now() / 9000)
.translate(250, 150, 0)
.resolution(this.#width, this.#height, 200);
this.#ctx.bindBuffer(this.#ctx.ARRAY_BUFFER, this.#ctx.createBuffer());
this.#ctx.bufferData(this.#ctx.ARRAY_BUFFER, coords, this.#ctx.STATIC_DRAW);
this.#ctx.vertexAttribPointer(positionAttr, coordBlockSize, this.#ctx.FLOAT, false, 0, 0);
this.#ctx.bindBuffer(this.#ctx.ARRAY_BUFFER, this.#ctx.createBuffer());
this.#ctx.bufferData(this.#ctx.ARRAY_BUFFER, colors, this.#ctx.STATIC_DRAW);
this.#ctx.vertexAttribPointer(colorAttr, colorBlockSize, this.#ctx.FLOAT, false, 0, 0);
this.#ctx.bindBuffer(this.#ctx.ELEMENT_ARRAY_BUFFER, this.#ctx.createBuffer());
this.#ctx.bufferData(this.#ctx.ELEMENT_ARRAY_BUFFER, coordIndex, this.#ctx.STATIC_DRAW);
this.#ctx.uniformMatrix4fv(transformUniform, false, transform.matrix);
this.#ctx.drawElements(this.#ctx.TRIANGLES, coordIndex.length, this.#ctx.UNSIGNED_SHORT, 0);
}
}
Y esto es todo por el momento, ¡por fin somos capaces de dibujar cosas en 3D moviéndose por la pantalla! ¡Broche de oro si además comprendes perfectamente cómo funciona! Y ahora un pequeño ejercicio de agudeza visual. De todos los colores definidos, hay uno que no llega a verse nunca. ¿Cuál es? ¿Qué cambiarías, tocando lo menos posible, para conseguir que se viera?