WebGL2 - Un poco de movimiento
Created at: 2023-03-26
Segundo tutorial de la serie de artículos dedicados a WebGL en su segunda versión. En este artículo aprenderemos los conceptos esenciales para conseguir animar a nuestros aburridos polígonos del primer artículo. Para ello, veremos una forma mejor de definir los vértices de nuestros polígonos, y aprovecharemos el cambio para conseguir moverlos a nuestro antojo de forma más sencilla.
Este es el resultado de lo que pretendemos conseguir.
Aquí tienes el enlace al repositorio con todo el código de esta serie de tutoriales.
Igual que con el artículo anterior, el código de este tutorial funciona perfectamente sin necesidad de tener un servidor web detrás. Así te vuelvo a recomendar que te lo descargues y juegues con él. Esta vez debería de resultarte un poco más sencillo entender qué está pasando; y si no, espero que ya no te queden dudas cuando termines de leer este artículo.
Si no lo has hecho ya, te recomiendo que leas antes este artículo acerca de cómo dimos movimiento a los aliens, pues la mayoría de las ideas para conseguir animaciones con javascript son las mismas. En resumen, animar figuras consiste en dibujarla figura muchísimas veces en pantalla en un segundo, cambiando un poco su posición cada vez. Hablaremos más de ello cuando veámos el código relacionado.
Álgebra
Uno de los objetivos de este artículo es cambiar el sistema de coordenadas del tutorial anterior, para evitar tener que recurrir a ese tan poco intuitivo rango de -1 a +1 que tiene el lienzo de dibujo de webgl2 por defecto. No creo que haga falta señalar lo horrible que sería calcular los vértices de figuras más complejas si siguiéramos por este camino.
¿Qué alternativas tenemos? Después de darle un par de vueltas, y con la idea de que dar movimiento a nuestros polígonos fuera igualmente sencillo, al final he optado por aplicar la misma solución estándar que la mayoría de programadores sigue para dibujar mundos en 3D. Pero es que es tan, tan, tan buena, que merece mucho la pena empezar a aplicarla ya mismo aunque estemos en 2D. ¿Y qué solución es esa? Pues ya hice spoiler en el titular de esta sección: Usaremos una de las ramas más potentes que nos proporciona las matemáticas: El álgebra. ¿Sigues ahí? ¿Hola?
Para sorpresa de nadie, renderizar videojuegos es cien por cien álgebra aplicada. No voy a entrar en detalles para no aburrir al personal, pero básicamente el álgebra nos proporciona un conjunto de herramientas que nos permite trabajar con números y letras de forma sistemática y organizada para resolver problemas más complejos. Es decir, dado una agrupación de datos de entrada (números) y siguiendo una secuencia de operaciones concreta, obtenemos el resultado esperado. Exacto, esto es una definición casi idéntica a la de algoritmo. De hecho, algoritmo y álgebra son palabras tan parecidas porque derivan del nombre de una misma persona, Al Juarismi, uno de los padres del álgebra y de la algoritmia. Sus primeros algoritmos no eran software, eran las explicaciones de cómo realizar muchas operaciones algebraicas para resolver problemas complejos pero cotidianos, como resolver ecuaciones de primer(x) y segundo grado(x2). Y hoy, 1200 años después, vamos a usar sus enseñanzas en nuestro videojuego.
Una de las herramientas algebraicas clave son las matrices. Una matriz es una agrupación bidimensional de números; en otras palabras, una tabla. Y sobre ellas, podemos aplicar todas las operaciones aritméticas básicas, como sumas, restas, multiplicaciones, divisiones... aunque con algunas reglas particulares. Por ejemplo, solo podemos sumar matrices que tengan el mismo tamaño (número de filas y columnas), y solo podemos multiplicarlas si el número de columnas de la primera coincide con el número de filas de la segunda.
Si recuerdas nuestras figuras del ejemplo anterior, un polígono es en esencia una colección de las coordenadas de sus vértices. Podríamos decir que un polígono es una matriz, así que ya estarás oliéndote la tostada. Situarla en cualquier lugar de la pantalla y moverla a nuestro antojo consiste en ejecutar algún tipo de operación algebráica sobre ella. ¡Eureka! En concreto, solo necesitaremos una operación: la multiplicación entre dos matrices.
La matriz de transformación
De forma más o menos general, nuestros polígonos 2D pueden realizar tres tipos de movimientos:
- Moverse por la pantalla, que llamaremos trasladar.
- Modificar su tamaño, que llamaremos escalar.
- Rotar un determinado ángulo.
¿Cómo podemos usar matrices para hacer cada una de estas operaciones? No hace falta calentarse mucho la cabeza, pues está tó inventao: Recurriendo a las matrices de transformación. Queda fuera del alcance de este tutorial la explicación y demostración matemática de cómo funciona cada una de estas operaciones. Me centraré en la aplicación práctica y en señalar algunos detalles importantes.
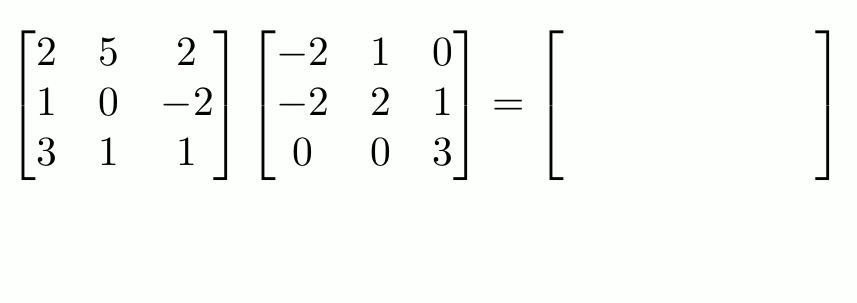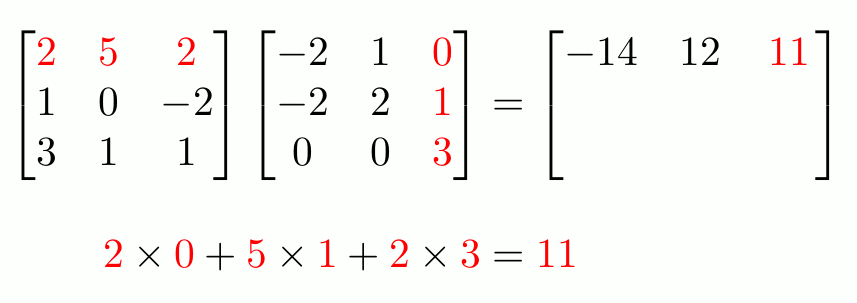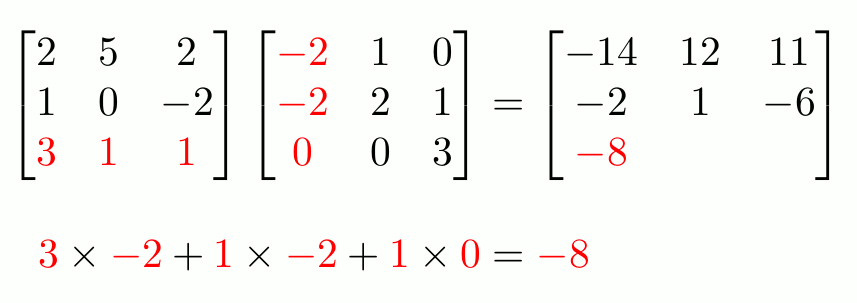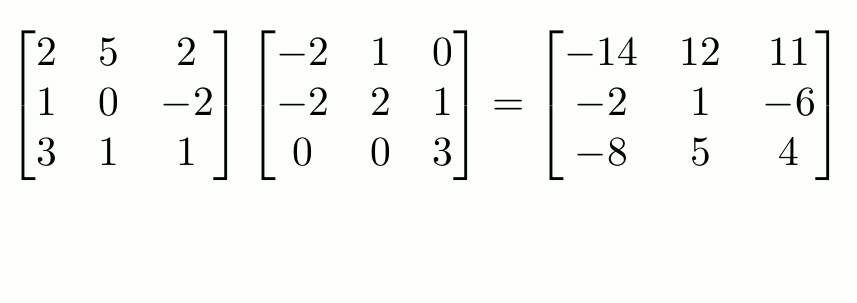
En resumen, realizar una traslación es multiplicar una matriz de coordenadas por otra matriz que contiene la distancia en cada dimensión. Rotarlo consiste en multiplicar la matriz de coordenadas por otra donde contiene el seno y el coseno del ángulo en radianes, dispuestos de forma concreta. Y escalar consiste en otra multiplicación con otra matriz que contiene los factores de escalado en cada eje.
Otra ventaja fundamental es que se pueden concatenar todas las operaciones en una sola matriz, que llamaremos matriz de transformación. Para conseguirlo, la matriz inicial sobre la que empezar a ejecutar multiplicaciones tiene que tener un valor neutral, es decir, un 1. En este contexto, se llama matriz de identidad, que consiste en una matriz llena de ceros excepto una de sus diagonales, que tienen unos. El resultado de multiplicar la matriz de identidad por cualquier otra es igual a esa segunda matriz. Finalmente, si multiplico esta matriz de transformación por otra con los vértices del polígono, aplicaré todos los movimientos (transformaciones) de golpe.
Así que voy a necesitar código para realizar todas estas operaciones con matrices. De esto se encargará la nueva clase Matrix3:
'use strict'
class Matrix3 {
#matrix;
constructor(matrix) {
this.#matrix = matrix;
}
get matrix() {
return this.#matrix;
}
rotate(rad) {
const c = Math.cos(rad);
const s = Math.sin(rad);
this.#matrix = this.#multiply(
[
c, -s, 0,
s, c, 0,
0, 0, 1
]
);
return this;
}
scale(sx, sy) {
this.#matrix = this.#multiply(
[
sx, 0, 0,
0, sy, 0,
0, 0, 1
]
);
return this;
}
translate(tx, ty) {
this.#matrix = this.#multiply(
[
1, 0, 0,
0, 1, 0,
tx, ty, 1
]
);
return this;
}
#multiply(other) {
return [
this.#matrix[0] * other[0] + this.#matrix[1] * other[3] + this.#matrix[2] * other[6],
this.#matrix[0] * other[1] + this.#matrix[1] * other[4] + this.#matrix[2] * other[7],
this.#matrix[0] * other[2] + this.#matrix[1] * other[5] + this.#matrix[2] * other[8],
this.#matrix[3] * other[0] + this.#matrix[4] * other[3] + this.#matrix[5] * other[6],
this.#matrix[3] * other[1] + this.#matrix[4] * other[4] + this.#matrix[5] * other[7],
this.#matrix[3] * other[2] + this.#matrix[4] * other[5] + this.#matrix[5] * other[8],
this.#matrix[6] * other[0] + this.#matrix[7] * other[3] + this.#matrix[8] * other[6],
this.#matrix[6] * other[1] + this.#matrix[7] * other[4] + this.#matrix[8] * other[7],
this.#matrix[6] * other[2] + this.#matrix[7] * other[5] + this.#matrix[8] * other[8]
];
}
static identity() {
return new Matrix3(
[
1, 0, 0,
0, 1, 0,
0, 0, 1
]
);
}
}
La idea es crear una matriz de identidad usando el método estático identity, para luego ir encadenando operaciones como rotate, scale y translate a nuestro gusto. Cada una de estas operaciones consiste en multiplicar la matriz actual por otra matriz 3X3 con los valores ordenados de una determinada forma. Para recuperar el resultado, tenemos el método getter matrix. La implementación de la multiplicación es la más directa posible, evitando iterar el array métodos for o forEach en busca de más rendimiento. Dijimos que las matrices son agrupaciones de dos dimensiones; sin embargo, estamos implementándolo con arrays de javascript de una sola dimensión. ¿Cómo es posible esto? Bueno, basta con jugar con los índices de forma ordenada, de forma similar a lo que hace webgl para gestionar los bloques de los búferes. Pero mucho ojo con esto: la multiplicación de matrices no es conmutativa, es decir, el orden en el que se hace las multiplicaciones, o lo que es lo mismo, en el que se aplican las transformaciones, es de vital importancia. Si las realizas en otro orden, el resultado será diferente.
El motivo de que la matriz sea 3X3 a pesar de estar en un contexto 2D, es que las operaciones tienen que ser lineales y homogéneas, y esto se consigue añadiendo una nueva dimensión neutra (con valor 1) tanto a la matriz de transformación como a cada vértice a multiplicar. ¿Te has quedado con la cara torcida? Intentaré explicarlo de forma más so menos sencilla.
Imagina que usamos matrices 2X2, pensemos en un vértice a transformar, por ejemplo (1, 2).
A este punto, quiero escalarlo, por ejemplo, a 3 en el eje x, y a 4 en el eje y. El resultado sería:
Matriz para escalar
[
2, 0,
0, 3
]
Coordenada a transformar
[1, 2]
Resultado
2 * 1 + 0 * 2 = 2
0 * 1 + 3 * 2 = 6
[2, 6]
¿Y qué pasaría con una matriz 3X3?
Matriz para escalar
[
2, 0, 0
0, 3, 0
0, 0, 1
]
Coordenada a transformar (le añado a la tercera posición el valor neutro 1)
[1, 2, 1]
Resultado
2 * 1 + 0 * 2 + 0 * 1 = 2
0 * 1 + 3 * 2 + 0 * 1 = 6
0 * 1 + 0 * 2 + 1 * 1 = 1
[2, 6, 1]
¡Dan el mismo resultado, ignorando el valor neutro! Sí, de acuerdo, para trasformaciones de escalado 2D, no necesitamos matrices de 3X3. Si repetimos las operaciones para las transformaciones de rotación, podemos comprobar que tampoco la necesitamos.
¿Pero qué pasa con las transformaciones de translación? Imagina que quiero moverla 2 unidades en el eje x, y 3 en el eje y. Hagamos primero la operación con la matriz 3X3:
Matriz para trasladar
[
1, 0, 0
0, 1, 0
2, 3, 1
]
Coordenada a transformar
[1, 2, 1]
Resultado
1 * 1 + 0 * 2 + 2 * 1 = 3
0 * 1 + 1 * 2 + 3 * 1 = 5
0 * 1 + 0 * 2 + 1 * 1 = 1
[3, 5, 1]
Bien, ahora probemos con una matriz 2X2... pero tengo un problema, ¿cómo la defino? Las dos primeras filas son equivalentes a la matriz de identidad... Probemos a meter los valores de la traslación en la última fila, sustituyendo el (0, 1) que le correspondería:
Matriz para escalar
[
1, 0,
2, 3
]
Coordenada a transformar
[1, 2]
Resultado
1 * 1 + 2 * 2 = 5
0 * 1 + 3 * 2 = 6
[5, 6]
¡Se obtienen resultados diferentes! Y si haces mentalmente el cálculo de la translación, que consiste simplemente en sumar el valor de cada coordenada de la translación con su misma coordenada del vértice, te darás cuenta de que el resultado usando una matriz 2X2 no es correcto.
¿Por qué pasa esto? La explicación matemática es que las transformaciones de escalado y rotación son lineales, pero la de traslación no lo es.
Un intento de explicarlo de forma visual, pero muy simplista, es imaginar que el polígono a transformar es un cuadrado, donde el origen de coordenadas (0, 0) corresponde a su centro. La operación de rotación y de escalado mueven todos los vértices manteniendo el centro en el mismo sitio, (0, 0), pero la operación de traslación evidentemente lo va a cambiar de sitio, asi que es una operación distinta a las demás.
Pero no te preocupes demasiado, este problema se resuelve de forma sencilla añadiendo una dimensión neutra a matrices y coordenadas.
Una pequeña librería de ayuda
Para limpiar un poco nuestra clase Engine de código boilerplate (código inicial básico y repetitivo, pero necesario, que se necesita para empezar una aplicación), vamos a mover toda la lógica para crear el programa a una nueva clase.
'use strict'
class Webgl {
static #createShader(ctx, type, source) {
const shader = ctx.createShader(type);
ctx.shaderSource(shader, source);
ctx.compileShader(shader);
if (!ctx.getShaderParameter(shader, ctx.COMPILE_STATUS)) {
console.error(ctx.getShaderInfoLog(shader));
throw 'Error in your shader';
}
return shader;
}
static createProgram(ctx, vertexShaderSource, fragmentShaderSource) {
const vertexShader = Webgl.#createShader(ctx, ctx.VERTEX_SHADER, vertexShaderSource);
const fragmentShader = Webgl.#createShader(ctx, ctx.FRAGMENT_SHADER, fragmentShaderSource);
const program = ctx.createProgram();
ctx.attachShader(program, vertexShader);
ctx.attachShader(program, fragmentShader);
ctx.linkProgram(program);
ctx.useProgram(program);
return program;
}
}
Es exactamente el mismo código del primer tutorial.
Usando matrices
Antes de entrar en la clase principal, me gustaría comentar por encima cómo vamos a usar las matrices de transformación. Antes dije que la idea era concatenar todas las operaciones de movimiento en nuestra matriz de transformación, para terminar multiplicándola por la matriz de vértices de cada polígono del juego.
Si hiciera estas multiplicaciones en el código de javascript y a nuestro vertex shader en GLSL le llegara la coordenada final, estaría desperdiciando toda la potencia que nos ofrece la GPU de la tarjeta gráfica. Dado que multiplicar matrices es una tarea pesada, es mucho mejor mover todas las operaciones posibles al vertex shader. La primera opción es crear variables uniformes por cada matriz que represente cada operación que quiera realizar, y hacer todas las multiplicaciones con GLSL. Esta solución sería óptima, pero muy engorrosa de gestionar con código en el lado de javascript.
Creo que la forma más balanceada para conseguir eficiencia sin que sea muy engorrosa de calcular, es hacer que javascript (CPU) concatene mediante multiplicaciones todas las operaciones a realizar sobre el polígono, y dejar que el vertex shader (GPU) se encargue de multiplicar cada vértice por la matriz de transformación. Como cada vértice lo definimos como de tipo vec2, tendremos que transformarlo a un vec3 para poder multiplicarlo con la matrix 3X3 de transformaciones, aprovechando la regla de que para multiplicar matrices no hace falta que tenga el mismo tamaño, que basta con que el número de columnas de la primera sea igual al número de columnas de filas de la segunda. De esta marea, javascript tendrá que hacer hasta tres multiplicaciones, una por cada posible transformación, mientras que GLSL tendrá que hacer una multiplicación por cada vértice, que con polígonos 3D complejos, pueden llegar a ser decenas de miles.
Teniendo todo esto en cuenta, no te sorprenderá la pinta que tiene el programa.
class Engine {
#ctx;
#program;
#width;
#height;
constructor(canvas) {
const vertexShaderSource = `#version 300 es
precision highp float;
in vec2 a_position;
uniform mat3 u_transform;
void main() {
gl_Position = vec4(u_transform * vec3(a_position, 1), 1);
}
`;
const fragmentShaderSource = `#version 300 es
precision highp float;
out vec4 outColor;
uniform vec4 u_color;
void main() {
outColor = u_color;
}
`;
this.#width = 400;
this.#height = 400;
canvas.width = this.#width;
canvas.height = this.#height;
this.#ctx = canvas.getContext('webgl2');
if (!this.#ctx) {
throw 'Your browser does not support webgl2';
}
this.#program = Webgl.createProgram(this.#ctx, vertexShaderSource, fragmentShaderSource);
this.#drawAll();
}
// ...
}
El fragment shader es el mismo, pero el vertex shader tiene un pequeño cambio: hemos añadido una nueva variable uniforme u_transform. Las matrices de 3 dimensiones se tipan como mat3 en GLSL. Aplicar la transformación es multiplicar dicha matriz por el vértice. Como el vértice es 2D, hay que transformarlo en un vec3 para poder multiplicarlo por la matriz, como comentamos anteriormente. Para transformarlo, le añadimos un 1, para no romper la homogeneidad de la multiplicación.
Y para crear el programa usamos la nueva clase Webgl, que mostramos anteriormente.
Añadiendo movimiento
Como explicamos en un tutorial anterior, para conseguir animar un juego necesitamos crear un bucle que llame contínuamente a métodos que dibujen cosas en la pantalla. Este bucle no puede hacerse con un while(true) porque el código no puede ser bloqueante, o el navegador se ahogará. Así que no nos queda otra que buscar alternativas, como setTimeout o setInterval. Esta solución requeriría indicar un tiempo en milisegundos, así que si lo ponemos alto, perderíamos el rendimiento de los ordenadores potentes, y si lo ponemos muy bajo, perjudicaría a ordenadores poco potentes. HTML5 trajo la solución definitiva, window.requestAnimationFrame, que es similar al setTimeout, pero esta vez el navegador se encargará de decidir cuánto tiempo esperar antes de ejecutar el callback indicado, según la potencia de la máquina.
Asi que para usar requestAnimationFrame, debemos crear un método que se únicamente se encargue de dibujar en pantalla nuestro mundo.
'use strict'
class Engine {
// ...
#drawAll() {
this.#ctx.viewport(0, 0, this.#ctx.canvas.width, this.#ctx.canvas.height);
const positionAttr = this.#ctx.getAttribLocation(this.#program, 'a_position');
const transformUniform = this.#ctx.getUniformLocation(this.#program, 'u_transform');
const colorUniform = this.#ctx.getUniformLocation(this.#program, 'u_color');
this.#drawLoop(positionAttr, transformUniform, colorUniform);
}
#drawLoop(positionAttr, transformUniform, colorUniform) {
this.#clear();
this.#drawTriangle(positionAttr, transformUniform, colorUniform);
this.#drawRectangle(positionAttr, transformUniform, colorUniform);
window.requestAnimationFrame(() => this.#drawLoop(positionAttr, transformUniform, colorUniform));
}
#clear() {
this.#ctx.clearColor(0, 0, 0, 1);
this.#ctx.clear(this.#ctx.COLOR_BUFFER_BIT);
}
// ...
}
Esto lo conseguimos partiendo el viejo método drawAll en dos partes. La primera creará los punteros del contexto que vamos a necesitar para mandar valores desde javascript a GLSL, y otro método drawLoop que hará de bucle infinito donde aplique los cambios. Para enviar la matriz de transformación, declaramos un nuevo puntero transformUniform.
Para que el resultado no resulte abrumador, en nuestro primer ejemplo que puedes ver aquí solo haremos una rotación.
Este sería el código para dibujar las figuras:
'use strict'
class Engine {
// ...
#drawTriangle(positionAttr, transformUniform, colorUniform) {
const blockSize = 2;
const coords = new Float32Array([
0, 0,
0, 0.5,
0.7, 0
]);
const totalBlocks = coords.length / blockSize;
const color = [1, 0, 0, 1];
const transform = Matrix3
.identity()
.rotate(Date.now() / 1000);
this.#ctx.enableVertexAttribArray(positionAttr);
this.#ctx.bindBuffer(this.#ctx.ARRAY_BUFFER, this.#ctx.createBuffer());
this.#ctx.bufferData(this.#ctx.ARRAY_BUFFER, coords, this.#ctx.STATIC_DRAW);
this.#ctx.vertexAttribPointer(positionAttr, blockSize, this.#ctx.FLOAT, false, 0, 0);
this.#ctx.uniformMatrix3fv(transformUniform, false, transform.matrix);
this.#ctx.uniform4fv(colorUniform, color);
this.#ctx.drawArrays(this.#ctx.TRIANGLES, 0, totalBlocks);
this.#ctx.disableVertexAttribArray(positionAttr);
}
#drawRectangle(positionAttr, transformUniform, colorUniform) {
const blockSize = 2;
const coords = new Float32Array([
-0.8, -0.8,
-0.8, -0.3,
-0.3, -0.3,
-0.8, -0.8,
-0.3, -0.8
]);
const totalBlocks = coords.length / blockSize;
const color = [1, 1, 0, 1];
const transform = Matrix3
.identity()
.rotate(Date.now() / -1000);
this.#ctx.enableVertexAttribArray(positionAttr);
this.#ctx.bindBuffer(this.#ctx.ARRAY_BUFFER, this.#ctx.createBuffer());
this.#ctx.bufferData(this.#ctx.ARRAY_BUFFER, coords, this.#ctx.STATIC_DRAW);
this.#ctx.vertexAttribPointer(positionAttr, blockSize, this.#ctx.FLOAT, false, 0, 0);
this.#ctx.uniformMatrix3fv(transformUniform, false, transform.matrix);
this.#ctx.uniform4fv(colorUniform, color);
this.#ctx.drawArrays(this.#ctx.TRIANGLE_STRIP, 0, totalBlocks);
this.#ctx.disableVertexAttribArray(positionAttr);
}
}
Las coordenadas de las figuras siguen siendo las mismas que las que pusimos en el primer tutorial. Pero esta vez, estamos creando una matriz de transformación transform a la que aplicamos una rotación de Date.now() / 1000. Puse este valor para que las figuras giraran a la misma velocidad (y una en negativo para que lo haga en sentido contrario), sin importar la potencia de tu máquina, y sin que haga falta usar la idea del tiempo delta en este sencillo ejemplo. He usado 1000 para que gire más lentamente. La importancia de este código radica en que estamos usando uniformMatrix3fv para enviar la matriz a GLSL. Su segundo extraño parámetro de tipo booleano sirve para indicar si queremos transponer la matriz, invertir sus ejes, es decir, convertir las filas en columnas y viceversa.
Si abres el ejemplo con este código, las figuras están girando de forma extraña... Si te fijas, verás que están girando usando la coordenada (0, 0) como centro. Esto no es nada útil. ¿Cómo lo arreglamos? Pues deberías imaginártelo. Si la rotación considera que el eje de giro es el orígen de coordenadas, habría que redefinir todas las coordenadas de la figura para que ese centro (0, 0) coincidiera con el centro geométrico de la figura. La rotación entonces funcionará correctamente... pero entonces todas las figuras se dibujarían en el centro de la pantalla, lo cual tampoco es nada útil. ¿Qué hacer? Exacto, trasladar la figura a su posición final después de rotarla.
Trasladando polígonos
Ok manos a la obra. Empecemos con el cuadrado, que es el caso más sencillo. Viendo las coordenadas que declaramos antes, se infiere que es un cuadrado de lado 0.5. Posicionar las coordenadas para hacer que su centro sea (0, 0) es sencillo, solo hay que ir poniendo valores 0.25 y -0.25 según el vértice que estemos definiendo. ¿Y a dónde lo muevo? Vuelvo a prestar atención a las coordenas, y calculo que su centro estaba abajo a la izquierda, exactamente en (-0.5, -0.5). Como antes de moverlo estaba en (0, 0), la cantidad a trasladarlo en cada eje coincide con la coordenada donde quiero posicionarlo.
'use strict'
class Engine {
// ...
#drawRectangle(positionAttr, transformUniform, colorUniform) {
const coords = new Float32Array([
-0.25, -0.25,
-0.25, 0.25,
0.25, 0.25,
-0.25, -0.25,
0.25, -0.25
]);
const transform = Matrix3
.identity()
.rotate(Date.now() / -1000)
.translate(-0.5, -0.5);
// ...
}
}
Por otro lado, el triángulo ya tiene su vértice inferior izquierdo en la coordenada (0, 0). Como no tengo ganas de determinar su centro y recalcular sus vértices, lo dejo como está, y que siga rotando sobre dicho vértice.
Puedes ver el ejemplo funcionando aquí.
Cambiando el sistema de coordenadas
Por último, queda por resolver el tema más peliagudo. Las coordenadas de los vértices y la cantidad de la translación en cada eje, está en el confuso sistema de unidades de webgl, que va de -1 a +1. Y para complicar más las cosas, la y crece hacia arriba, no hacia abajo. ¿Es posible usar como referencia el eje de coordenadas que teníamos en el canvas 2D, donde el orígen (0, 0) corresponde a la esquina superior izquierda del canvas, y además poder indicar las medidas (al escalar) en píxeles?
Bueno, tenemos varias formas de encarar el problema, pero yo he optado por la siguiente: El tamaño final del canvas puede variar, asi que mejor si las coordenadas de los vértices de los polígonos son totalmente independientes de dicho tamaño. Esto se resuelve haciendo que el orígen de coordenadas (0, 0) quede en el lugar que me interesa (a menudo, el centro del polígono), y que sus vértices tengan posiciones normalizadas. ¿Qué quiere decir esto? Significa no hay que pensar en píxeles, si no situar los vértices de tal forma que la distancia de referencia es la unidad, para que más adelante cuando escale la figura, indique cuántos píxeles mide exactamente cada unidad de distancia. En un cuadrado, por ejemplo, es hacer que la distancia entre cada par de vértices que forman un lado sea una unidad.
Así que por el momento, defino mi polígono de forma normalizada, lo escalo para que tenga el tamaño que me interesa, lo roto porque de eso va el tutorial, y lo traslado para situarlo en la posición donde me interesa que esté su centro. Ahora toca resolver el problema de cambiar el sistema de coordenadas.
En este momento, tengo los vértices de los polígonos situados en posiciones absolutas como yo quería, es decir, el origen de coordenadas corresponde al vértice superior izquierdo del canvas donde quiero dibujarlos. Pero sabemos que webgl no funciona de esta forma, asi qué hay que volver a hacer algo para convertir esas coordenadas a otras donde el vértice superior izquierdo corresponda a la posición (-1, 1), y resolviendo además el problema de la deformación de pasar un canvas HTML posíblemente rectangular a un contexto webGL con forma cuadrada, como explicamos en el primer tutorial. Espero que algún avispado lector se haya dado cuenta de que en esencia esto implica dos transformaciones: Un escalado para resolver el problema del tamaño de los polígonos, y una traslación para el problema de mover el orígen de coordenadas.
¿Cuánto escalo por ejemplo el eje x? Sé que el ancho del contexto webgl mide 2, ya que forma un cuadrado que va desde (-1, 1) de su vértice superior izquierdo al (1, -1) de su vértice inferior derecho, ya mencionado en el primer tutorial. Calcular el valor final de cualquier coordenada es aplicar una simple regla de 3. Imagina que mi canvas mide 600X400, y quiero saber como transformar la coordenada (300, 200), es decir, su centro, al sistema de coordenadas de webgl.
WEBGL --> CANVAS
------------------
2 --> 600
webgl_x --> 300
webgl_x = 300 * 2 / 600 = 1
O de forma genérica
webgl_x = canvas_x * 2 / canvas_width
2 --> 400
webgl_y --> 200
webgl_y = 200 * 2 / 400 = 1
O de forma genérica
webgl_y = canvas_y * 2 / canvas_height
Imaginando que el vértice superior izquierdo de webgl es (0, 0), la solución es (1, 1) parece correcta... si no tengo en cuenta de que en webgl la y crece hacia arriba. Para arreglar este inconveniente, simplemente tengo que invertir el eje y, es decir, multiplicarlo por -1. Así resuelvo definitivamente el problema, escalando cada vértice por (2 / width, 2 / height * -1), o lo que es lo mismo, (2 / width, -2 / height).
Bien, si aplico la corrección al cálculo anterior, tenemos la coordenada en (1, -1). Para hacer que dicha coordenada del ejemplo anterior, que recordemos que corresponde al centro del canvas, corresponda también al centro del contexto de webgl, solo hay que trasladarla una unidad hacia la izquierda y otra unidad hacia arriba, o lo que es lo mismo, trasladarla una cantidad (1, -1) de unidades.
Para no tener que repetir este cálculo en cada polígono, he preferido añadir estas nuevas transformaciones au nuevo método de nuestra querida Matrix3, y si no has colapsado por el camino, te habrás imaginado que su implementación es:
'use strict'
class Matrix3 {
// ...
resolution(width, height) {
return this
.scale(2 / width, -2 / height)
.translate(-1, 1);
}
// ...
}
Solo resta modificar la clase Engine para aplicar todas estas ideas. He modificado también el tamaño del canvas a un rectángulo de 600X400 en lugar de ul anterior cuadrado de 400X400, para demostrar que la definición de los polígonos es ahora totalmente independiente del tamaño y la relación de ancho / alto del canvas:
'use strict'
class Engine {
// ...
this.#width = 600;
this.#height = 400;
// ...
#drawTriangle(positionAttr, transformUniform, colorUniform) {
const coords = new Float32Array([
0, 0,
0, -1,
1.4, 0
]);
const transform = Matrix3.identity()
.scale(100, 100)
.rotate(Date.now() / 1000)
.translate(200, 200)
.resolution(this.#width, this.#height);
// ...
}
#drawRectangle(positionAttr, transformUniform, colorUniform) {
const coords = new Float32Array([
-0.5, -0.5,
-0.5, 0.5,
0.5, 0.5,
-0.5, -0.5,
0.5, -0.5
]);
const transform = Matrix3.identity()
.scale(100, 100)
.rotate(Date.now() / -1000)
.translate(90, 310)
.resolution(this.#width, this.#height);
// ...
}
}
Someramente, declaro los vértices de ambas figuras para normalizar más o menos sus vértices y aplico las siguientes transformaciones a cada polígono:
- Lo escalo para que la unidad mida 100 píxeles.
- Lo roto para dar un poco de vida al escenario.
- Lo traslado para que su centro esté donde me interesan.
- Aplico el nuevo método de resolución para cambiar el sistema referencial del eje de coordenadas.
El resto de código es el mismo. Como curiosidad, la corrección del cambio de dirección del eje y provoca que las figuras roten en el sentido contrario a los ejemplos anteriores... nadie es perfecto.